Bulk Semaphore: Garden-Variety NFT Auctions and zkTrees

Mohamed El Tahawy (Blockframe) & Omar Yehia (Matter Labs)

TL;DR

• Current auction systems for NFTs on the blockchain often fall short, leading to mispriced NFTs, market inefficiencies, and failure to meet key auction objectives such as maximizing revenue for sellers.

• Sealed-bid auctions, where bids and bidders remain confidential, address these issues. The idea is multiple bidders placing confidential bids on an NFT, backed by collateral, can establish a strong market consensus for the NFT's value. They are proven to be credible, optimal and strategy-proof when implemented on a public ledger for certain buyer valuations [4]. However, they were impossible to implement in a blockchain setting due to prohibitive gas costs — until now with our solution.

• Blockframe introduces Bulk Semaphore, a scalable protocol for bulk anonymous membership and signaling made possible via zkTrees. In this paper, we demonstrate how we use this protocol to conduct sealed bid auctions.

• The zkTree model emerges as a scalable and efficient solution for bulk verifying zero knowledge proofs on a public ledger like Ethereum. zkTrees allow for us to conduct an unlimited number of sealed-bid auctions, each with no limit on the number of participants, and the cost of on-chain verification for an entire auction is constant regardless of the number of bidders.

• Blockframe's Bulk Semaphore protocol is feature-agnostic and can be extended to other use-cases such as trade auctions and anonymous DAO voting.

• In addition to using sealed bid auctions to conduct NFT trades, they will be available as a MEV-aware minting strategy in Blockframe's Creator Studio. This renders gas wars obsolete and also means NFTs can be priced accurately based on real demand from the moment minting begins.

View a live demo of Blockframe’s sealed bid protocol here: https://blockframe.io/sealed-bids-demo

About Blockframe.io

Blockframe is an upcoming marketplace for non-fungible tokens (NFTs). Our ecosystem introduces on-chain royalties, AI-assisted collection creation tools at scale, and an NFT perpetuals exchange, enabling users to interact with the NFT market in new formats. Our platform is based on three tenets: 

1. Creators come first

2. An incentivized and engaged user base

3. Removing barriers to entry into the NFT market

Blockframe will launch an alpha version in August 2023. We will release a separate article formally introducing our platform and detailing all of its features.

Prelude

NFT Marketplaces like Blockframe, Blur, and OpenSea typically use Continuous Double Auctions (CDA) to conduct NFT trades. In this format, buyers and sellers are continuously making offers and creating listings — a transaction is executed when an offer is equal to or greater than a listing price.

This paper evaluates CDAs through the lens of game theory demonstrating that CDAs reach a suboptimal Nash Equilibrium. In the context of CDA auctions, bidders do not bid their true valuation of an item and sellers do not receive the maximum revenue they can achieve. Specifically, the CDA model falls short in achieving these key auction objectives:

• Revenue Maximization: The auction design should aim to provide the highest possible return for the seller.

• Incentive Compatibility: The auction design should encourage all participants - bidders, the auctioneer, and the seller - to act in accordance with their true valuations and intentions. For bidders, this means bidding in line with their true valuation of the item not influenced by strategic behavior. For the auctioneer and seller, this means conducting the auction in a fair and transparent manner, without manipulation of the process or the bids.

• Collusion Resistance: The auction design should discourage participants from coordinating their bids to manipulate the outcome of the auction in their favor.

• Social Welfare Maximization: The auction design should ideally ensure the NFT goes to the buyer who values it most.

When these objectives are not met, the auction fails to realize socially optimal outcomes—situations where both buyers and sellers simultaneously maximize their utility functions. This failure results in mispriced NFTs, creating inefficiencies in market liquidity and distorting the allocation of resources. Consequently, both buyers, who may overpay, and sellers, who may not receive a fair return, end up experiencing losses. This underscores the need to explore alternative auction formats that can better address these objectives.

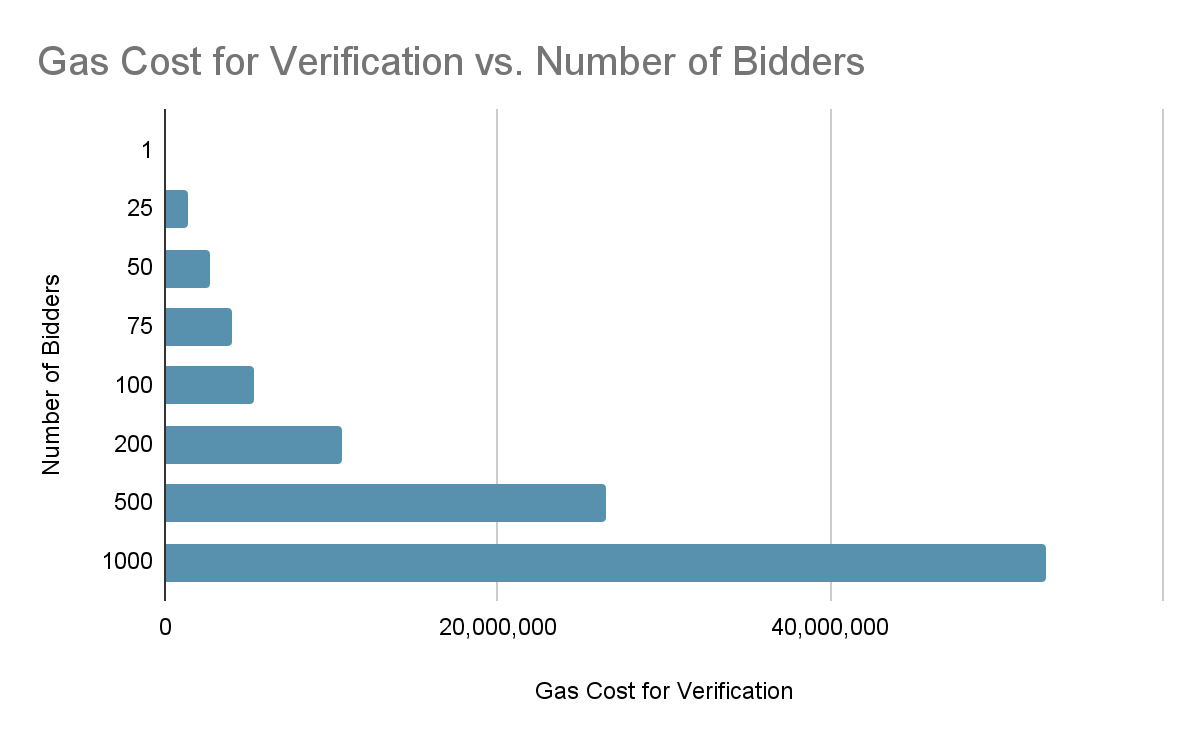
The option we delve into is the sealed-bid auction where bids and bidders remain confidential for the duration of the auction. However, implementing this auction type within a blockchain context poses a significant challenge: how can you maintain bid confidentiality in a public ledger? This challenge has been a focal point of research for several years, as the cost of implementing such a system has typically proven too prohibitive. A sealed bid auction implementation based on Consensys' Anon-Zether—a mixer for Ethereum and ERC20 tokens—consumes 10M gas to operate a single auction, with gas cost doubling for each doubling of the number of bidders [1]. A subsequent solution using range proofs is able to conduct an auction of 512 bidders for 2.3M gas [2]. Despite the optimizations employed by the authors, both these implementations carry infeasible costs — at the time of writing, 10M gas was priced at $1,800 and 2.3M at $414.

In this article, Blockframe presents a scalable protocol for bulk anonymous membership and signaling. We demonstrate its capabilities in a real world setting by adapting it to conduct sealed bid auctions on Blockframe. This protocol is able to support an unlimited number of sealed-bid auctions, each with no limit on the number of participants within the limitations of the blockchain.  Furthermore, the protocol is generic and can be extended to other use-cases such as anonymous DAOs which we intend to implement as well. The rest of this article offers a comparative analysis of CDA and sealed-bid auctions and then a deep dive into how we achieved this milestone via zk-SNARKs and more specifically zkTrees.

Comparative Analysis of CDA and Sealed-Bid Auctions

Our first model auction scenario is a Continuous Double Auction (CDA) where bids and asks are publicly available. This involves one seller (S) and four buyers.

The seller's NFT carries no cost in terms of utility.

\(\begin{align*} \text{Seller's NFT utility value (}v_s\text{):} & \quad 0 \\ \end{align*} \)

The buyers have maximum valuations that follow a specific order.

\(\begin{align*} \text{Buyers:} & \quad b_1, b_2, b_3, b_4 \\ \text{Max valuations:} & \quad v_{b1} = w, v_{b2} = x, v_{b3} = y, v_{b4} = z \\ \text{Order:} & \quad w < x < y < z \end{align*}\)

We assume each buyer is aware of the other’s maximum valuation as this is the case in a blockchain setting. For example, one can extract a list of bidders for a particular NFT collection, calculate their total balances and recursively compute the balances of wallets that have funded them to find out an approximate maximum valuation which would allow them to underbid in an auction.

Each buyer's utility is the difference between their valuation and the price they paid, or 0 if the price exceeds their valuation, represented as:

\(\begin{equation} U_i = \begin{cases} v_i - p & \text{if } v_i > p \\ 0 & \text{otherwise} \end{cases} \end{equation}\)

The seller's utility aligns directly with the selling price:

\(\begin{equation} u_s = p \end{equation} \)

Proposition: The unique Nash Equilibrium of this game is achieved when each buyer bids their respective value, ensuring they outbid those buyers who could be outbid by them but avoid overbidding the buyers who could outbid them.

Proof: In order to establish a Nash Equilibrium, we need to demonstrate that no buyer can increase their utility by unilaterally changing their strategy. Given the ordered set of buyers where each buyer, understanding that they cannot outbid any of the buyers with higher valuations, optimally chooses never to bid more than their own maximum valuation.

\(B = \{b_1, b_2, b_3, b_4\} \quad \text{where} \quad v_{b_i} < v_{b_{i+1}} \)

Meanwhile, each buyer is aware of the maximum valuations of those buyers who could outbid them and ensures they outbid these buyers but avoid overbidding the buyers who could outbid them.

\(\beta_{b_i} = \min\{v_{b_i}, p_{i+1} + 1\} \quad \text{for all} \quad i \in \{1, 2, 3, 4\} \)

Following these strategies, none of the buyers have an incentive to deviate from their bid, fulfilling the conditions for a Nash Equilibrium.

The auction concludes with the NFT going to the highest bidder. The course of the auction unfolds as follows: 

• b₁ and b₂ increase their bids up to their maximum valuations (w and x respectively).

• b₃ aware of b₂'s maximum valuation, strategically bids x+1.

• b₄ aware of b₃’s maximum valuation, strategically bids y+1.

Therefore, b₄ wins the auction with a bid of y+1.

However, this Nash Equilibrium yields outcomes that fall short of meeting desirable auction objectives:

• Revenue Maximization: The seller earns y + 1, despite b₄'s willingness to pay up to z.

• Incentive Compatibility: The optimal strategy for each participant doesn't align with their true valuation.

• Collusion Resistance: CDAs are not collusion resistant. For instance, if bidders b₃ and b₄ collude, they could agree that b₃ will not bid above x. In return, b₄ could agree to pay (y-x)/2 to b₃ as an incentive for not outbidding them. This collusion allows b₄ to win the auction at a lower price of x+1, which is still profitable for them even after the payment to b₃.

• Social Welfare Maximization: The NFT goes to b₄, who values it the most, thereby maximizing social welfare.

We will now explore the same example in the context of a Vickrey Auction (with reserve price), a type of sealed-bid auction. In a Vickrey Auction, the highest bidder wins but pays the second-highest bid or the reserve price set by the seller, whichever is higher. Let's denote the reserve price as 𝑟, where 𝑟 ≤ 𝑧. If b₁, b₂, b₃, and b₄ bid their maximum valuations, b₄ wins the auction, but pays the maximum of b₃'s bid of 𝑦 and the reserve price 𝑟. The other key difference is that in all sealed bid auctions, bids and bidder identities are sealed.

Let's consider the Nash Equilibrium for this type of auction:

Proposition: In a Vickrey Auction, bidding one's true valuation is a dominant strategy, leading to a Nash Equilibrium.

Proof: Suppose a buyer decides to bid less than their maximum valuation. If their bid is less than the maximum valuation of any other buyer, then they lose and obtain a utility of 0, which is lower than the utility they would have obtained by bidding truthfully.

\(\text{If } b < v_{b_j} \text{ for any } j \neq i, \text{ then } U_i = 0 \)

If their bid is greater than the maximum valuation of all other buyers, then they still win, but the final price remains the same (equal to the second highest bid or the reserve price), so the utility doesn't change.

\(\text{If } b > v_{b_j} \text{ for all } j \neq i, \text{ then } U_i = v_{b_i} - \max(v_{b_{j \neq i}}, r) \)

Therefore, bidding less than one's maximum valuation is never beneficial. Bidding more than one's maximum valuation risks overpayment if the second highest bid or the reserve price exceeds their own valuation. Hence, bidding one's true valuation is the dominant strategy, and all players doing so constitutes a Nash Equilibrium.

The auction concludes with NFT going to 𝑏₄ for a price of the maximum of 𝑦 and 𝑟 set by the seller. This format addresses the issues seen in CDAs:

1. Revenue Maximization: The seller earns the maximum of 𝑦 and 𝑟, which could potentially be 𝑧 or greater. This potential for higher revenue exists despite the fact our CDA scenario assumed perfect information symmetry, whereby bidders were aware of each other’s valuations, a condition that is rarely met in real-world scenarios.

2. Incentive Compatibility: Buyers are incentivized to bid their true valuations because underbidding could result in losing an item they value more than the price paid, while overbidding could lead to overpaying.

3. Collusion Resistance: Since bids are not publicly disclosed, the participants could not strategize based on the knowledge of other bidders’ maximum valuations. For example, in our scenario, even if 𝑏₃ and 𝑏₄ wanted to collude, they would not know the exact bids of 𝑏₁ and 𝑏₂.

4. Social Welfare Maximization: The NFT goes to 𝑏₄, who values it the most, thereby maximizing social welfare.

It is also worth noting the work of Chitra et al. [4] who have studied the implementation of such auctions, also known as Deferred Revelation Auctions (DRAs), over a secure, censorship-resistant ledger like a blockchain. They demonstrated that the DRA is not only credible but also optimal and strategy-proof for α-strongly regular distribution valuations, as long as α > 0. In addition, as per Akbarpour and Li in 'Credible Optimal Auctions' [5], a first-price auction with a properly set reserve price can be the unique static credible optimal-revenue auction. And while, this comes at the cost of losing the dominant strategy property, because bidders in a first-price auction need to shade their bids based on their beliefs about the distribution of other bidders' valuations. It is possible to obtain a strategy-proof counterpart of the first-price auction using the revelation principle, known as the "shading" auction, which preserves the good properties of the first-price auction, including revenue maximization and credibility, while also being strategy-proof.

Therefore we conclude that Continuous Double Auctions, despite their prevalence, can result in suboptimal outcomes for both buyers and sellers. Specifically, the revenue realized by the seller can be less than what the buyer with the highest valuation was willing to pay, leading to lost potential revenue. The auction format is not collusion resistant allowing for buyers to manipulate prices which can deter potential new entrants due to lack of trust in the market, thereby reducing allocative efficiency and market liquidity. Furthermore, the bidding strategies in a CDA don't align with a buyer's true valuation which can lead to strategic bidding, where buyers bid less than their true valuation to avoid overpaying, further impacting revenue maximization.

In contrast, Vickrey Auctions, where each participant is incentivized to bid their true valuation, often achieve a socially optimal outcome. These auctions are strategy-proof, meaning that the dominant strategy for each bidder is to bid their true valuation, regardless of what they believe other bidders might bid. By ensuring participants bid their true valuations, these auctions prevent market manipulation, providing a reliable system for price discovery. This inspires confidence in both existing participants and attracts potential new entrants, who can trust that prices truly reflect the perceived value of the NFTs being traded. The strategy-proof and socially optimal nature of Vickrey auctions creates a system that is more conducive to the discovery of fair value for NFTs.

Unlocking Sealed-Bid Auctions on Blockchain with zk-SNARKs

The main challenge in implementing a sealed-bid auction in a blockchain setting is ensuring data confidentiality for bid values and bidder identities for the duration of the auction. Current cryptographic methods employed on Ethereum, such as the ECDSA signatures, are effective in confirming data authenticity, i.e., this message was indeed signed by Alice but do not offer a way to hide Alice’s message.

Data confidentiality is the exact problem space that zkSNARKs, or 'Zero-Knowledge Succinct Non-Interactive Argument of Knowledge', are designed to address. These proofs allow one party (the prover) to demonstrate to another party (the verifier) that they know a specific value x, without revealing any information beyond the fact they know the value x. 

zk-SNARKs, applied to our sealed bid auction scenario, would allow an auctioneer to confirm the validity of a bidder's commitment, without ever seeing it and whilst keeping it hidden from other bidders thereby satisfying the data confidentiality requirement of conducting a sealed bid auction.

zk-SNARKs: Link to the Blockchain

To generate a zk-SNARK requires the creation of an arithmetic circuit – a representation of a mathematical computation that can verify certain properties about the computation's input and output. For each circuit, a prover and a verifier are created. The prover generates a proof from a particular input (referred to as a 'witness'), and the verifier allows any party to check the validity of the proof without ever revealing the witness.

In the context of our discussions, we assume the verifier is deployed as a smart contract on Ethereum, it takes in a proof as a parameter and returns whether the supplied proof is valid based on the publicly available witness generator. The verifier is the ultimate bottleneck in a system like this because it lives on the blockchain and incurs a gas cost per computation step.

In the next sections, we will examine three implementations of sealed-bid auctions, illustrating how the friction of these implementations outweighs their cost of implementation, after which we will describe our implementation via zkTrees.

Naive Implementation 1: Single zk-SNARK Proof per Bid

In this straightforward approach, the auctioneer creates a Circom circuit that takes in a bid value and a bid secret, hashing them to represent a bidder’s commitment. The bid secret adds a layer of security, preventing any 'brute-force' attempts to guess the bid by systematically checking all possible values

When the user is ready to make a bid in an auction, the witness generator is used to generate a proof from the user’s witness (inputs). In the case of a WASM-based witness generator, it would live in the browser. After the bidding phase of the auction is complete, the bidders proceed to reveal their bid amounts to the auctioneer by supplying their bid value, secret and original proof. The auctioneer can then use the verifier to verify the revealed bids serially, select a winner and complete the auction. 

Analysis

The gas cost per bid proof verification in this example is 53,000 gas assuming the use of Circom and snarkjs. This means that for the auctioneer to verify a single auction with 100 bidders, it would cost 5M gas or $1,000 at the time of writing this article. We ignore all off-chain costs such as the prover and server costs associated with the zkSNARK as they are negligible comparative to the on-chain costs.

Naive Implementation 2: Single-Circuit zk-SNARK

The major issue with the former approach is the repeated calls to the verifier, specifically verifying a single bid equates to a single verifier call. What if we could conduct an auction and verify all the bids at once by submitting a single proof? This naive solution involves a single zk-SNARK circuit that takes as input a list of bids (as before, each bid is represented by a bid value and a bid secret), a list of bid proofs and outputs the highest bid value and the proof of the highest bid:

When the user is ready to make a bid in an auction, the witness generator is used to generate a proof from the user’s witness (inputs). The auctioneer will store the users’ bid values, secrets and proofs off-chain and off-circuit. After the bidding phase of the auction is complete, the auctioneer can then use the verifier to verify all the bids at once, select a winner and complete the auction.

Analysis

While this solution is an improvement from the previous since it allows an auctioneer to submit a single proof to validate the entire auction, it has several flaws:

1. This solution requires the auctioneer to keep track of the bids off-chain and off-circuit, violating auction credibility as it is no longer incentive compatible for the auctioneer to follow the rules.

2. This circuit requires a maximum number of bidders to be provided beforehand. This is because the proving key and verification key generated for a circuit can only later accept input shaped in the same size and format as the original circuit. In other words, this means each verifier deployed on-chain can only handle auctions with a specific number of bidders. This can be solved by expecting the circuit to receive an extra number of placeholder nodes/empty bids.

3. The number of inputs to the circuit is a function of the number of bidders. Therefore, the gas cost to verify an auction increases linearly with the number of bidders.

In this approach, verifying a single auction with 12 bidders consumes 393,503 gas which equates to about $100 at the time of writing this article. While a significant improvement, this implementation is limited by a cap on the number of bidders as the cost of gas increases significantly as the maximum number of bidders the system can support increases. What if we wanted to support 100 simultaneous bidders? This approach instantly becomes infeasible. We ignore all off-chain costs such as the prover and server costs associated with the zkSNARK as they are negligible comparative to the on-chain costs.

Alternative Implementations:

In examining alternative implementations, we have turned our attention towards a private on-chain voting protocol introduced by a16z called Cicada, based on homomorphic time-lock puzzles, described here.

To use Cicada to implement a sealed-bid auction we would create a time-lock puzzle for each bid. The RSA modulus for this puzzle is specifically chosen such that it would take exactly the duration of the auction to brute-force on a single CPU core. In practice, ensuring that the bid (the solution to the puzzle) can only be computed after the auction has ended.

Let’s assume we are using the AWS EC2 instance x2iedn.metal with 128 CPUs, costing $27 per hour. We can compute solutions for 128 different bidders simultaneously over a 24-hour period, leading to a computational cost of $648. From this, we can calculate the cost per bidder per day: $648/128 bidders = approximately $5.06. To support 65536 bidders, this would result in a cost upwards of $100,000 per month which is infeasible.

zkTree: The Scalable Solution for Sealed-Bid Auctions

An elegant solution is nested within a data structure called zkTree which is discussed at length by the team at Polymer Labs who coined the term in the zkTree literature [3]. Essentially, a zkTree is a Merkle tree where every node in the tree is a zkSNARK, and each parent node recursively proves its children's zkSNARKs. 

Consider the practical application of a zkTree to a sealed-bid auction. Let’s create a zkTree for each auction and as the auction unfolds, each bid is translated into a zkSNARK proof that is inserted into the tree. Whenever there are n bids, where n is the maximum number of children per node, they are combined into a parent node. This procedure repeats recursively up the tree until the tree converges into a single root node. This node is a zkSNARK proof that guarantees the correctness of all n child proofs and their children and so on and so forth. Essentially, the root becomes a proof of proofs that if verified guarantees the validity of all the bids in an auction. This means that in order to verify an entire auction, the auctioneer just needs to verify the root node, paying constant gas and the price of just one verification operation! 

We will now focus on our implementation details and how we used a zkTree to implement our sealed bid auction protocol. The end goal is to create a witness generator for our users to generate bids, and a prover for the root node of our zkTree with its corresponding verifier deployed on-chain. We used Plonky2 to develop the code for the circuit and prover. We then used Polymer Labs’ plonky2-circom repository to convert our root node proof to a Plonky2 Circom circuit that we deploy to Ethereum. As part of these implementation details, it's important to define the structure of each node in the tree, which we'll refer to as the 'bid proof'.

The Bid Proof

Just like in the naive approaches, we may be tempted to store a bid value and a bid secret, the challenge is that a user might claim they're placing a bid of 1 ETH and submit a corresponding proof, but we lack a mechanism to ensure that they will indeed pay 1 ETH when the auction ends. This makes the system vulnerable to Sybil attacks and bad actors. To resolve this, we will collect the user’s bid upfront as collateral that will be reimbursed should they lose the auction. In order to prevent the user’s address from being publicly visible when making this transaction over a public ledger, the sealed bid protocol smart contract will serve as a mixer expecting to receive a collateral and a bid commitment. 

This is the exact use-case of Semaphore – a framework for zero-knowledge signaling minimally consisting of the following components:

• Secret Key (sk): A unique value that is randomly generated. It should be known only to the user.

• Public Key (pk): Derived from the secret key, the public key is represented as H(sk, 0), where H is the Poseidon Hash.

• Signal/Topic (topic): This is the bid value.

• Nullifier (n): This serves as a unique identifier for each bid, which is computed as H(sk, topic). The nullifier is also used to prevent double bidding and to withdraw deposits for losing participants at the end of the auction.

In this zkSNARK system, each participant in the auction has a corresponding leaf in a Sparse Merkle tree, associated with their public key, which is derived from unique private keys known only to them. This structure allows for secure and efficient identity verification of bidders without revealing their private keys.

A circuit then verifies whether the signal (the bid) was validly produced by a participant. This verification is done by checking the nullifier, a unique identifier for each bid, and verifying the Merkle proof indicating the participant knows a private key that corresponds to a public key in the Sparse Merkle tree.

First, we create a Merkle tree for the Semaphore framework, this is just an example Merkle tree and will have to be modified as per the protocol design, for example in a real world scenario, you may want to use a nullifier and trapdoor in place of a single randomly generated private_key:

Next we define our semaphore circuit, adapted from plonky2-semaphore:

1. First we define the field over which the zkSNARK computations are performed, we are using a Goldilocks Field with a Poseidon Hash, and 2nd degree polynomials:

2. Create a CircuitBuilder and PartialWitness.

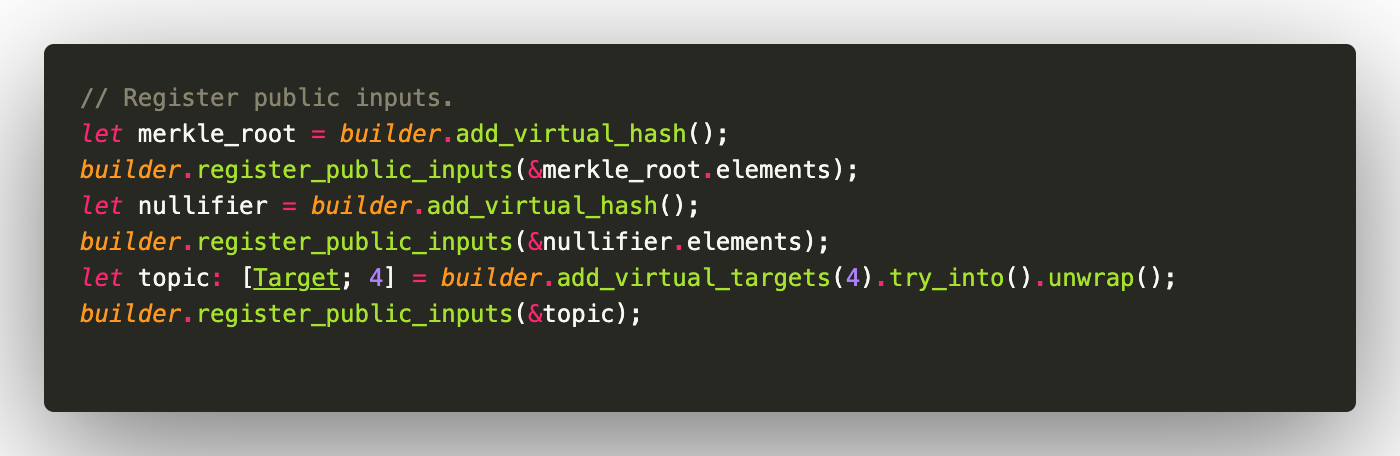
3. Register public inputs: merkle_root, nullifier and signal/topic.

4. Prepare and verify Merkle tree proof. This is checking that the public key, represented by the hashed secret key, is part of the Merkle tree rooted at merkle_root.

5. Verify the nullifier which serves as our bid commitment posted on-chain:

6. Return targets to be set by the PartialWitness.

7. Fill circuit targets with inputs: public_key_index, private_key and topic. These hashes can later be used to verify inclusion in the Merkle tree from step 3.

8. Build the circuit, create the proof and verify output.

This represents a single bid proof in our auction. The next step is to insert this proof into our zkTree which is a completely separate Merkle tree consisting of ZK proofs.

Root Node Prover

Next, we create our zkTree adapted from polymerdao/plonky2.

1. First, let’s define our zkTree constructor, this expects a CircuitConfig and a predefined tree depth. The tree depth/size is required upfront because remember, the proving key and verification key generated for a circuit can only later accept input shaped in the same size and format as the original blueprint computation. For a symmetrical system like proving a group of ED-25519 proofs, a small fixed size zkTree can be created and proofs can be verified in batches. However, in our case, we need to prove all the bids for an auction at once. The solution we adopt to fulfill this requirement is to create a larger zkTree with empty placeholder nodes. We store the zkTree in a binary heap like structure like so:

2. Based on the zkTree literature, we need to wrap each proof in a LeafProof, this method expects a proof and its related data (verifier data and common circuit data) and wraps it in a LeafProof. A hash is generated from the inner proof's public inputs and the circuit digest of both the inner verifier data and the current verifier data. This hash is used to link the leaf to its respective proof and verifier data:

3. The next step is to combine n (2 in our example) LeafProofs into a NodeProof. This process takes two sibling nodes (their proofs and verifier data) and creates a parent node that represents their combined information. The verifier data for this new node is a hash generated using the circuit digests from the left and right nodes' verifier data, and the current circuit's digest. This process effectively connects the parent node to its child nodes, creating a hierarchy within the zkTree:

4. We tie it all together by creating our insert and insert_recursive functions which receive a proof and its associated data, wrap it in a LeafProof and insert it into the tree at its corresponding index:

On-chain Verifier

After the blueprint computation zkTree is finalized:

1. Wrap root node in a Goldilocks field and BN128 field based Poseidon Hash recursive proof for compatibility with Circom and eventually Ethereum:

2. Use PolymerLabs plonky2-circom methods to convert root node to a Circom verifier:

3. The generated files can be used in PolymerDao/plonky2-circom to generate a Circom circuit that is capable of verifying a root node proof of a zkTree with the same structure as the one used to generate the circuit. The input to this circuit is the output from the root node prover we created in the last section.

4. The Circom circuit can be converted to a solidity verifier via snarkjs and Groth16’s Solidity verifier library.

System Overview

Implementation

Commitment Phase

1. Seller posts NFT for sale putting it up as collateral as well as locking in an optional reserve price.

2. Each interested participant submits a bid proof from an arbitrary address and a collateral amount that is fixed for all participants.

   1. The same collateral pool is used for all of Blockframe’s sealed bid auctions, so increases in the reserves of the collateral pool cannot be tied to a specific auction. The user should be able to deposit and withdraw from the sealed bid protocol smart contract using a bid commitment from any public ledger address, thereby creating a disconnect on-chain between a user address, specific auction and bid value.

   2. Each auction has its own Semaphore Merkle tree, i.e. “group”.

      1. The root hash is posted on-chain and the tree is maintained in the zkSNARK system.

Reveal Phase

1. After the conclusion of the auction, the bidders reveal their bids and secrets. The auctioneer uses these to compute the bid proofs for each bid and inserts them into a zkTree matching the zkTree structure used to create the circuit:

   1. The auctioneer wraps each bid proof into a leaf proof and groups them into n tuples. Each n tuples of leaf proofs are used to generate a root proof. The root proof verifies that all bids in the n tuples are correctly formed and supplied.

   2. The auctioneer continues this process of grouping leaf proofs into tuples and generating root proofs from each tuple until a single root proof remains representing the proof of all bids in the auctions.

   3. A security tradeoff can be made here to improve the user experience, the bidder can submit with their bid proof in step 2, a signed transaction encrypted with the auctioneer’s public key that can be executed to reveal a bid automatically. The downside is that this violates auction credibility as the auctioneer can see the bids before the auction is over thus it is no longer incentive compatible for the auctioneer to follow the rules.

2. This final root proof is verified on-chain publicly by the auctioneer to verify the authenticity of the auction and a winner is selected in Vickrey auction fashion.

3. Bidders who did not win the auction can generate a nullifier to make a withdrawal from an arbitrary address for a specific bid commitment.

Auditability

The nullifier for each bid is stored in a Merkle tree on-chain mirroring the Sempahore zkSNARK system Merkle tree. The root proof of the zkTree Merkle tree for every auction is recorded on-chain along with the root hash of the Semaphore “group” Merkle tree of the auction such that anyone can verify that a bid was included in a particular auction by checking its Merkle path from the root.

Analysis

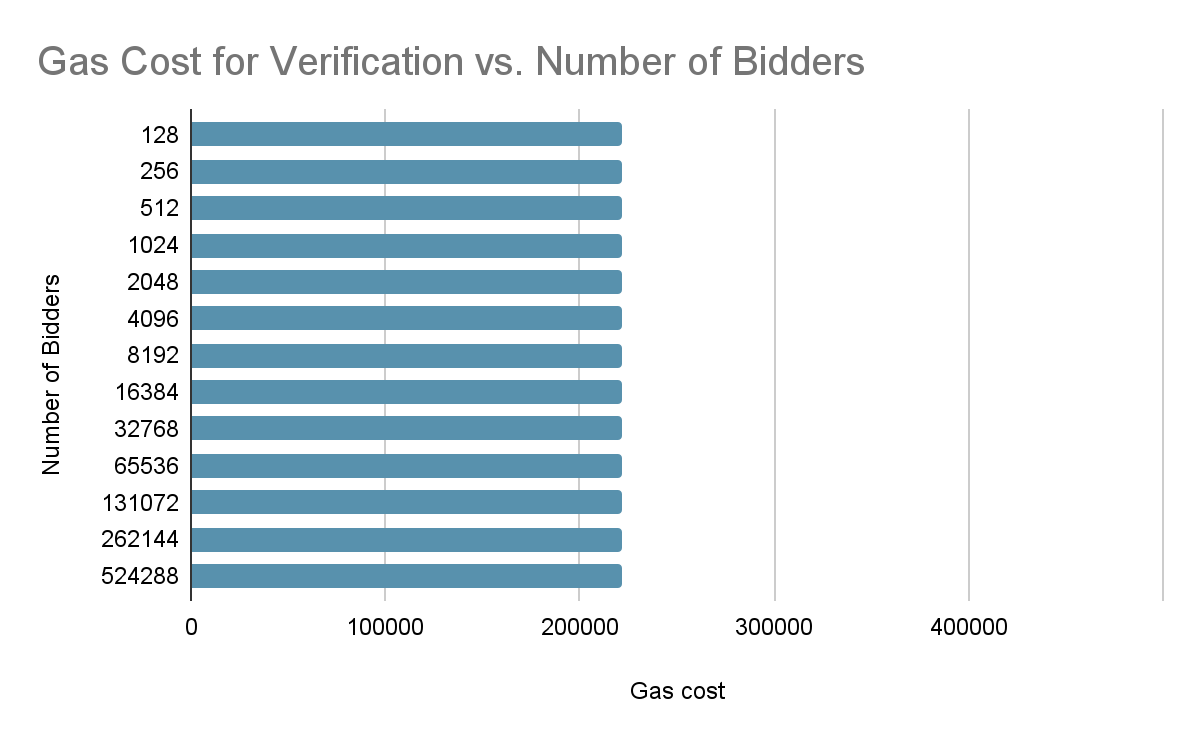
In this zkTree-based solution, the input to the verifier is always just a root proof node which contains links to its children via its circuit digest, verifier data and public inputs. This means the auctioneer only needs to submit and verify a single proof for an entire auction, therefore the runtime complexity of on-chain verification of an entire auction is always O(1) or constant regardless of the number of bidders!

The gas cost per root node verification is 221,665 assuming the use of Circom, Groth16’s Solidity verifier and Plonky2. We ignore all off-chain costs such as the prover and server costs associated with the zkSNARK as they are negligible comparative to the on-chain costs.

This means the cost of gas for verifying a sealed-bid auction is comparable to that of a decentralized exchange swap which is a common user interaction and typically consumes 100,000 - 200,000 gas.

Within the limitations of the blockchain, the zkTree solution scales to accomodate any number of bidders and any number of simultaneous auctions, and it also achieves this at a fraction of the cost compared to the previously explored implementations. Combining this with its O(1) utilization of gas for on-chain verification, the zkTree model emerges as a scalable and efficient solution for conducting bulk proof verification and sealed-bid auctions on a public ledger like Ethereum.

Source code

Bulk Semaphore: Open-source GitHub link to be posted following Blockframe’s launch.

What can I do with this?

Our scalable protocol for bulk anonymous membership and signaling is feature-agnostic. While we showcase its usage here for sealed-bid auctions, this protocol is generic and can be used to implement mixers, anonymous voting DAOs, anonymous surveys, identity verification and more.

Furthermore, the concept of zkTrees illustrated here can be used generally to bulk verify any type of proof. Take for example a root proof that verifies that a set of 50 images were generated by a large language model, or trade auctions such as the one used in stock exchanges where orders to buy or sell securities are collected over a certain period of time and then matched at a single price that maximizes the volume of trades.

Next Steps

• Develop a granular and standardized NFT pricing mechanism leveraging the property of bidders bidding their true valuation in a sealed bid auction.

• Use sealed bid auctions as a MEV-aware minting strategy in Blockframe's Creator Studio, customizable by creators. This renders gas wars obsolete and also means NFTs can start to be priced accurately based on demand from the moment minting begins.

• Use Bulk Semaphore in Blockframe’s DAO to leverage zero knowledge proof off-chain anonymous voting.

• Multi-Unit Vickrey Auctions

• Design the 'shading' auction mentioned above in the context of the Vickrey auction’s revenue maximization.

• Leverage zero knowledge proofs as well as account abstraction to implement larger intent and preference spaces for sealed bid auctions and other auction formats on Blockframe:

  • i.e. If NFT X is listed for sale, bid Y on chain A

Acknowledgements

We thank Porter Adams and Aviv Yaish from Matter Labs for their valuable feedback and insights on auction design.

Sources

[1] M. Kokaras and M. Foti, "The cost of privacy on blockchain: A study on sealed-bid auctions," Journal of Computational Science, vol. 54, Jan. 2023. [Online]. Available: https://www.sciencedirect.com/science/article/pii/S2096720923000088.

[2] Q. Zhang, Y. Yu, H. Li, J. Yu, and L. Wang, "Trustworthy sealed-bid auction with low communication cost atop blockchain," Information Sciences, vol. 502, pp. 315-328, Jun. 2023. [Online]. Available: https://www.sciencedirect.com/science/article/abs/pii/S0020025523002633.

[3] S. Deng and B. Du, "zkTree: A Zero-Knowledge Recursion Tree with ZKP Membership Proofs," [Online]. Available: https://eprint.iacr.org/2023/208.

[4] T. Chitra, M. V. X. Ferreira, and K. Kulkarni, "Credible, Optimal Auctions via Blockchains," [Online]. Available: https://eprint.iacr.org/2023/114.

[5] M. Akbarpour and S. Li, "Credible Auctions: A Trilemma," [Online]. Available: https://web.stanford.edu/~mohamwad/Credible.pdf.